Perpetual Motion (Narcotic)
Now that I've programmed my computer to play Perpetual Motion, I tell people that I've made a Perpetual Motion machine!
I tested 15 different versions of the game, and found that the win rate can vary considerably as a result of the particular rules being used.
Standard Rules and Variations
Normally I link elsewhere to a page describing the rules of each game, but I haven't found any online source that I think does a good job of describing this game, so I wrote my own here. This seems to be the most frequently described version, being consistent with most sources on the Internet, and matching those described by the excellent books The Penguin Book of Patience by David Parlett, and The Complete Book of Solitaire and Patience Games by Morehead and Mott-Smith. Some rule variations have been described in various sources, including:
Make Moves Left to Right
In The Book of Solo Games, Gyles Brandreth says to move cards of the same rank towards the right. In The Complete Patience Book, Basil Dalton does not mention a direction, but the example game shows moves in both directions, which implies that the player may choose.
Left to Right Pile Collection
Left to right collection of piles (between rounds) is described in the book 150 Ways to Play Solitaire by Alphonse Moyse, Jr., as well as the rules used in Matthew C. Clarke's paper On the Chances of Winning the game of "Perpetual Motion". Effectively, Wikipedia allows you to collect from left to right as well, because even though it says to collect piles from right to left, it allows you to collect them face down, which has the identical effect as if you collect the piles from left to right while still face up.
Not Allowing Recursive Moves
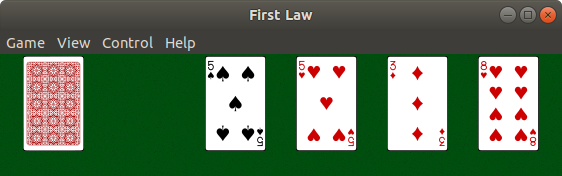
"Recursive moves" are moves which may become available only after other moves have been made (thus uncovering additional cards). For example, assume in the screenshot shown on top that the Eight of Clubs is under the Five of Hearts, and the Three of Spades is under the Eight of Hearts. After moving the Five of Hearts to the Five of Spades, the Eight of Hearts would be moved on top of the Eight of Clubs, revealing the Three of Spades, which would then be moved on top of the Three of Diamonds. But Matthew C. Clarke's program was configured to not make recursive moves, so only the Five of Hearts would be moved in this case.
Allow Not Making Moves
Most sources do not directly state that you must make every move you can, but this is usually implied. However, various software implementations (including BVS Solitaire Collection and Aisleriot, among others) allow the player to pass up moves. In fact, the Aisleriot help even encourages the user to consider doing so, in order to prevent a situation in which the game never ends.
Face-up Stock Dealing
Pretty Good Solitaire uses the standard pile stacking between rounds (right to left), but then deals the next round with the stock still face up! In other words, the order of the deck is reversed.
Column Discards
The books A New Book of Patience Games by Ernest Bergholt, and The Complete Patience Book by Basil Dalton both describe a Perpetual Motion variation called "Fours" in which discards of four cards of the same rank occur immediately when they form at the end of a pile, without having to hope they align correctly for discarding when dealt during the next round. It helps for the piles to be dealt overlapping downwards (rather than squared) in order to more easily identify when this happens.
Test Results
One billion deals were simulated for each variation tested. There were no inconclusive results.
Standard Deck Results
Win rates of standard deck variations of Perpetual Motion
| Version | Described By | Average
Rounds | Games
Won | Win
Rate % |
|---|
| Standard Rules | Morehead & Mott-Smith,
David Parlett | 44.7 | 86,691,579 | 8.6692
± 0.0017 |
| Left to Right Pile Collection | Alphonse Moyse, Jr. | 29.6 | 436,955,813 | 43.6956
± 0.0031 |
| No Recursive Moves | | 137.9 | 38,336,269 | 3.8336
± 0.0012 |
Left to Right Pile Collection,
and No Recursive Moves | Matthew C. Clarke | 129.2 | 548,033,229 | 54.8033
± 0.0031 |
| Make Moves Left to Right | Gyles Brandreth | 47.9 | 326,156,991 | 32.6157
± 0.0029 |
| Face-up Stock Dealing | Thomas Warfield | 34.9 | 319,281,737 | 31.9282
± 0.0029 |
| Allow Not Making Moves | Rosanna Yuen | N/A | 1,000,000,000 | 99.9999998
± 0.0000002 |
| Column Discards | | 13.8 | 811,427,224 | 81.1427
± 0.0024 |
The standard variation is winnable approximately 8.67% of the time.
Using Matthew C. Clarke's rules (left to right pile collection and not making recursive moves) resulted in the completion of about 54.8% of deals, which is consistent with his previous result.
Clearly, the order of pile collection makes a significant difference for the win rate. Collecting from right to left instead of left to right drops the win rate from 43.7% down to 8.67%. When not allowing recursive moves, this drop is even more remarkable: from 54.8% down to just 3.8%!
Piquet Deck Results
In A New Book of Patience Games, Ernest Bergholt suggests playing the game using a Piquet pack (a 32-card deck of eight ranks), because a full deck "often becomes extremely tedious". Basil Dalton describes using the Piquet pack as well in The Complete Patience Book.
Win rates of piquet deck variations of Perpetual Motion (or "Fours")
| Version | Described By | Average
Rounds | Games
Won | Win
Rate % |
|---|
| Piquet (8-rank) Deck | | 23.1 | 109,480,086 | 10.9480
± 0.0019 |
Piquet (8-rank) Deck,
and Column Discards | Ernest Bergholt | 6.8 | 826,845,356 | 82.6845
± 0.0023 |
Piquet Deck, Column Discards,
and Move Either Direction | Basil Dalton | N/A | 999,999,996 | 99.9999994
± 0.0000004 |
As expected, using a shortened 8-rank deck (Piquet pack) resulted in a faster game, with about half the number of rounds on average. The win rate also increased (to nearly 11%), although not by as much as anticipated.
Two-deck Results
Perpetual Motion can be played using two decks of playing cards. If sticking with four piles, it is necessary to make twice as many discards (two of each rank). Alternatively, eight piles may be used with the requirement of discarding all eight cards of the same rank at a time. These versions were tested in order to determine whether "Double Perpetual Motion" might be a viable game, and if so, how much longer it might take to play.
Win rates of two-deck variations of Perpetual Motion
| Version | Average
Rounds | Games
Won | Win
Rate % |
|---|
| Two Decks, 4 Piles | 54.5 | 72,382,600 | 7.2383
± 0.0016 |
| Two Decks, 8 Piles | 53.7 | 47,521,695 | 4.7522
± 0.0013 |
Two Decks, 4 Piles,
and Column Discards | 17.5 | 806,743,066 | 80.6743
± 0.0024 |
Two Decks, 8 Piles,
and Column Discards | 8.2 | 944,008,478 | 94.4008
± 0.0014 |
The 4-pile and 8-pile versions of using two full decks both proved to work fairly well, adding only about 10 rounds to the game on average. However, keep in mind that it takes longer to deal and play each round than when using a single deck. Both versions reduced the win rates, although by less than anticipated. As expected, using the Column Discards rule greatly shortened the games and increased the win rates.
Effect of Pile Collection Order on Winnability Rate
As previously noted, the win rate is much lower when using right to left pile collection between rounds. The reason is because stable patterns can more easily develop, and there is a single pattern that is responsible for a majority of the losses. The last card of the deck tends to get stuck at the end for a while, until it's able to jump to the left. But the first card is fixed in place until all four of that rank are discarded. It is fairly common to get three cards of the same rank at the beginning (in which case all three are fixed there), but then the fourth one has a hard time connecting. Since it cannot jump left, it tends to bounce around towards the end of the deck. Each time the last card of the deck is able to jump left, the new last card is disproportionately likely to be that fourth card of the same rank as the first three. If this situation happens at any time during the game, all four cards are locked into their positions and the game is doomed to eventually hit a repeating cycle. Even if the fourth card never reaches the end, it may still never connect with the three in front, and therefore lead to a repeating cycle (loss) anyway. The following is an example deal:
Round 1
| 9 | 10 | 7 | Q |
| 3 | K | 6 | Q |
| 4 | A | 8 | 3 |
| 6 | K | Q | J |
| 5 | 2 | J | 2 |
| 9 | 4 | K | 10 |
| 8 | A | 7 | 7 |
| 5 | K | 5 | 6 |
| 2 | 3 | 8 | 9 |
| 2 | 10 | J | 6 |
| 9 | 10 | 4 | 7 |
| 8 | Q | 3 | 5 |
| 4 | A | J | A |
Round 13
| 9 | 9 | 9 | 9 |
| 7 | 7 | 7 | 4 |
| 4 | 4 | A | A |
| 2 | 2 | 2 | 5 |
| 5 | 5 | 5 | K |
| K | J | J | J |
| K | K | 4 | 3 |
| 3 | 10 | 10 | 10 |
| 8 | 8 | 10 | Q |
| Q | 6 | 6 | 6 |
| 8 | 8 | J | A |
| A | 3 | 3 | Q |
| 7 | Q | 6 | 2 |
Round 20
| 7 | 7 | 7 | 4 |
| 4 | Q | Q | 8 |
| 8 | 6 | 6 | 10 |
| 10 | 10 | 2 | 2 |
| 2 | 3 | 3 | 3 |
| Q | Q | 8 | 8 |
| 4 | 4 | A | A |
| A | J | J | 5 |
| 5 | 5 | 5 | A |
| 10 | 3 | 6 | 6 |
| 2 | J | J | 7 |
In the illustration above, each set of four cards dealt during a round are shown in their own row (from top to bottom in the order dealt). Suits do not make a difference in this game, and therefore only the ranks are shown. All available moves are made in accordance with the standard rules, but are not shown.
The game starts with a Nine fixed at the beginning of the deck. In round 13, the four Nines are discarded, which results in three Sevens becoming locked at the front. In round 20, the fourth Seven is locked at the end, ensuring that the game will never complete. If you choose to continue the game, it will extend for another 58 rounds until a repeating cycle is eventually found (round 77 is repeated indefinitely).
Winning Every Game
Some sources incorrectly estimate that Perpetual Motion can eventually be won every time (or nearly so). But when using Aisleriot rules that allow the option of passing up moves, all billion deals tested were indeed completed (won)! Also, there were only four losses when playing by Basil Dalton's rules which allow moves in either direction (in each case, there were no moves available during the entire game). Furthermore, these wins were found by trying different choices only after encountering a repeated round, suggesting that a combination of clever play and/or trial-and-error should allow human players to win nearly every game as well.
Final Thoughts
Since the win rates and other statistics of this game (total number of rounds, etc.) vary so much depending upon the exact rules, it is important that any source describing the game should cite the correct statistics which apply to the game (and any variations) being described.
Thanks to Matthew C. Clarke for his helpful feedback for this article, and thanks to Michael Keller for identifying some classic solitaire books which describe Perpetual Motion.
Any comments are welcome, please send to:

Last modified October 4, 2022
Main page
Copyright ©2024 by Mark Masten. All rights reserved.

